Conversión Binaria

Los sistemas de numeración son un conjunto de símbolos y reglas que permi­ten representar datos numéricos, existen varios sistemas de numeración, pero solo nos concentraremos en dos sistemas y como convertirlos de binario a decimal y de decimal a binario.

• Sistema Binario

Este sistema utiliza sólo dos dígitos: 0 y 1. El valor de cada posición se obtiene de una potencia de base 2, elevada a un exponente igual a la posición del dígito menos uno.

• Sistema Decimal

Es un sistema de numeración posicional en el que las cantidades se representan utilizando como base el número 10, por lo que se compone de diez dígitos diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

• Sistema hexadecimal 

Es un sistema de numeración posicional de base 16.
Los símbolos que se usan en este sistema son:  0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Conversión 

Para poder comprender los dispositivos de red y las direcciones, primero hay que considerar los datos de la manera en que lo hace un dispositivo; en notación binaria, ya que cada número entre los puntos en una dirección IP se compone de 8 dígitos binarios (00000000 a 11111111

Para la conversión binaria, hablaremos de tres formas para la conversión a sistema binario.

(Estos métodos los utilizaremos para saber el valor de cada octeto de la dirección IP)

Primer Método:

Del número que se necesita convertir, solo se divide entre dos (una división sucesiva (X/2)), pero se debe tener en cuenta que:

1. Si el número a dividir no tiene residuos, entonces se pondrá un 0.
2. Si el número a dividir tiene residuos, entonces se pondrá un 1.

Ejemplos: 

Segundo Método:

Para este método utilizamos 

2ⁿ = x 

Donde necesitamos despejar a la "n" para saber cuantos números significativos (espacios o bits) necesitamos para formar el número binario y "x" es el numero decimal a convertir. 

Ejemplos: 

2ⁿ = 370   

2ⁿ= 370

Como necesitamos despejar “n” y "n" es un exponente utilizamos las leyes de los logaritmos
Por tanto nos quedara de la siguiente forma:

Ejemplo 2: 

Tercer método:

Para este método utilizamos una división entre una base hexadecimal es decir:

x / 16 

Donde "x" va a ser el número a convertir a binario.

Ejemplo:

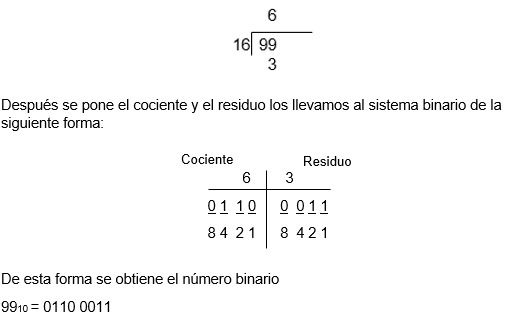
 Existen más métodos para convertir del sistema decimal al sistema binario, pero les presentamos lo que podrían ser los más fáciles y sencillos de hacer.